[TOC]

不同激活函数的表现

现在我会展示一下激活函数的不同会导致什么样的拟合现象，我创建了一些散点，它们大致表现为函数 $y=2sinx$，我相信这个函数的图像对你而言非常清晰，我在每个点的 $y$ 值上随机地进行了标准正态分布的随机数加减以打散它们。

在下面的图 3 我画了一条红色的线，那是通过统计学的最小二乘法公式得来的（赞美数学），如公式 1，你可能会觉得很复杂，这还是一元一次的情况，在更高维度下，求解公式会越来越复杂，幸好，我们的神经网络就是解决这个问题的，它提供了一个替代方法逼近原函数。

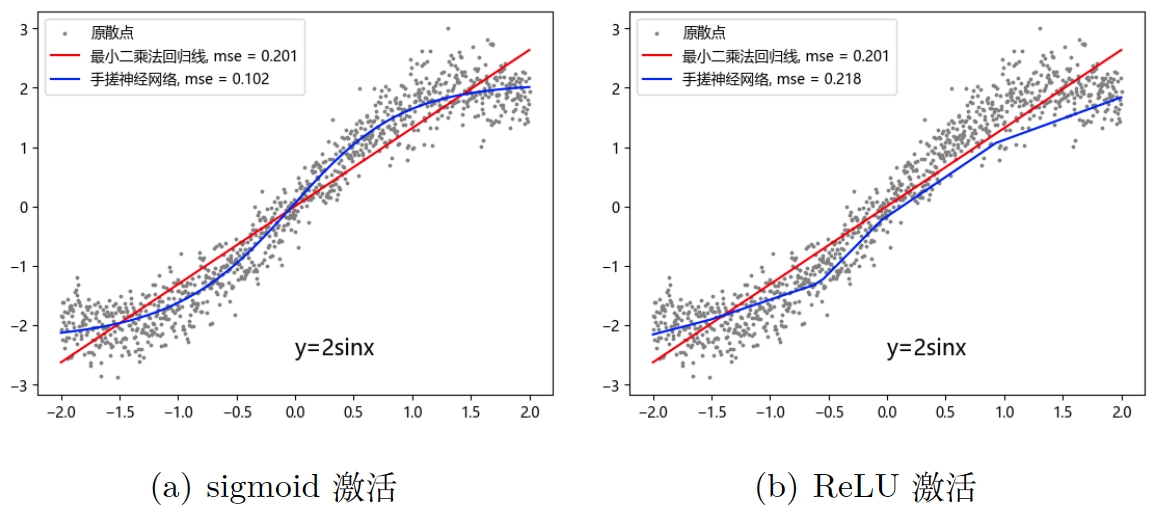
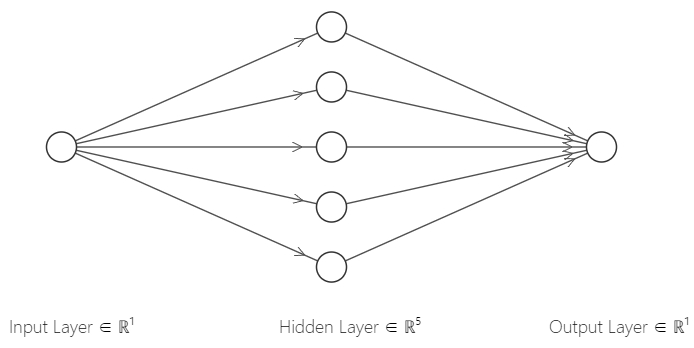
同时我手搓了一个隐藏层有五个神经元的神经网络，我建议你也定一个目标，即未来某一天写出自己的神经网络，这可是你吃饭的家伙！这个手搓网络的结构正如图 1，它有一个输入层，一个隐藏层，一个输出层，其中输入层是没有参数的，就是 $x$。当激活函数是 sigmoid 的时候，它表现得很好，如图 3（a），因为图像本身就是 s 型，用 s 型的激活函数自然表现最好，但我用 ReLU 时，它用几段折线的组合去拟合散点，理论上应该有 5 根折线，对应 5 个神经元，也表现得不错（吗），但是如果我使用更多神经元，如 100 个神经元，我们会有 100 个小线段，这种拟合对复杂的数据关系表现会更好，但也可能过拟合，如图 2 最右边的图示。此外，增加层数也可以有很大的提升，增加一层神经元就可以加一维的分类或拟合的能力，以此类推，试想两个面包片上下夹在一起，垂直划分是不可能分开的，但是水平切一刀就可以分开，这就是增加神经网络层数的作用。

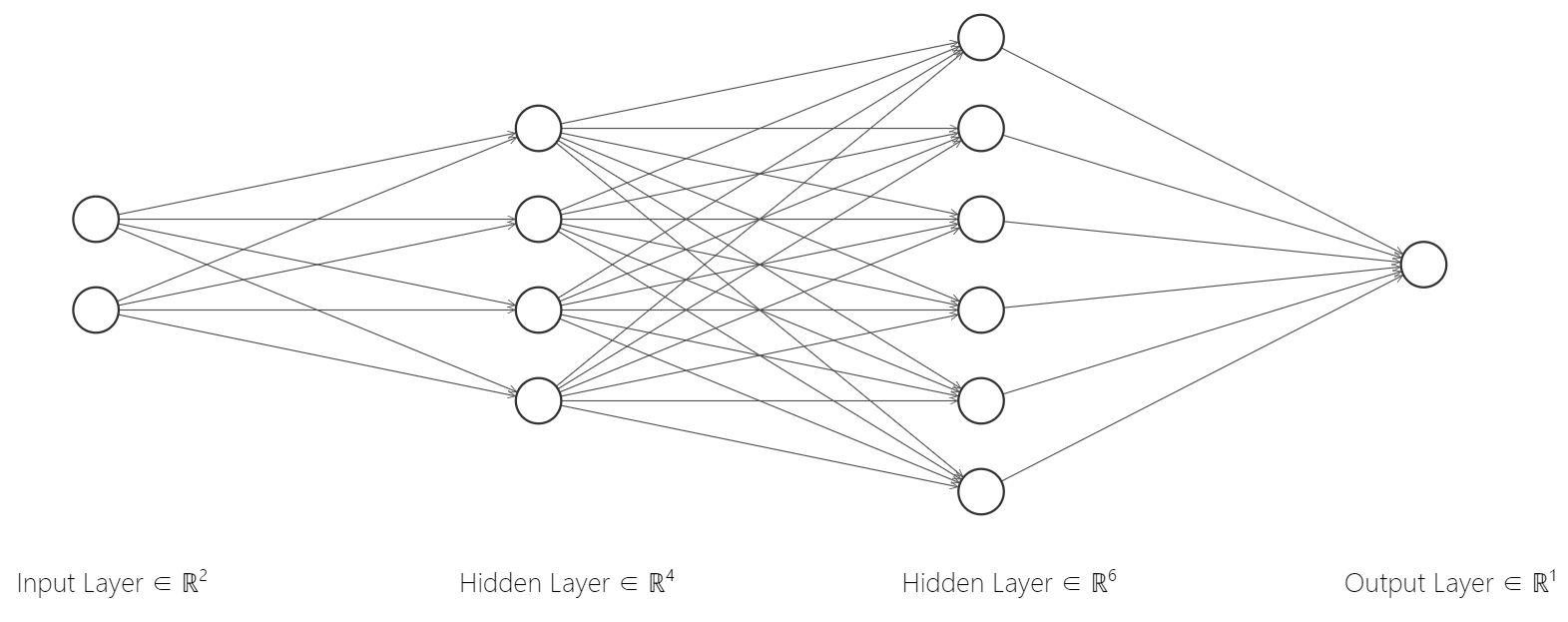
神经网络也可以更复杂，如上图，从左往右看，它有一个输入层，包含 2 个神经元，对应 2 个特征，两个隐藏层，各有 4 个和 6 个神经元，一个输出层，包含 1 个神经元，表示输出 1 个值，输入层没有参数，所以一般不认为是单独的一层，而隐藏层和输出层有参数，每一个神经元的的数量等于上一层神经元数量，但是一个神经元只有一个。

我们可以做一个简单的计算：一层有 4 个神经元，二层有 6 个神经元，那么二层就有 $4\ast 6+6=30$ 个需要估计的参数，其中 4 是一层神经元个数，6 是二层神经元个数，因此二层有 24 个不同的 $w$，加 6 是因为二层层每个神经元各有一个 $b$，也叫偏置项。

正向传播

观察图 4，数据从神经网络的左边进入，通过神经元计算传递到下一层神经元，最后从最右边的神经元输出一个值或矩阵，在机器学习领域，这些在神经网络中流动的矩阵，我们通常称为张量 （大多数人习惯把二维数组称为矩阵，高维数组称为张量，但是有时候可以混用，如一维张量，也就是向量；二维张量，也就是矩阵；三维张量等）。这些神经元是全连接的，即每一个神经元都要与下一层所有神经元连接起来，因此也可以称之为全连接神经网络，其含义与 MLP 基本一样。这里我们有两个隐藏层，它具有划分三维数据的能力，用来处理二维数据更是绰绰有余。

机器学习所需的数据，形式上类似常见的那些表格，我们规定一列为一个特征，或者称字段（虽然特征和字段所指代的东西基本相同，但不同场合仍然有不同叫法），假如我们现在有一份数据，它有三个字段，前两个是模拟考试 A 和 B 的分数，第三个是期末考试的分数，如上表，实际上在深度学习任务中，你大部分时候都要准备这样的表格，例如 xlsx 或者 csv 格式的表格，它必须包含若干特征列，并且包含一个目标列，通常是最后一列，例如这里的期末考试成绩，你必须有若干条这样的已知数据，例如 100 条甚至 10000 条，才能用于训练网络，因为网络是通过迭代来训练参数的，如果数据太少，迭代就难以进行，泛化能力也就不理想，通常我会用 70%的数据训练，15%的数据用于验证，15%的数据用于测试，这些数据不能混淆，在一开始就应该做出区分，否则称为数据集污染。

假如此时模型的任务是通过两次模拟考试的分数推断期末考试的分数，我们需要训练模型，单个输入的大小就是[2, 1]，也就是两行一列的二维张量，想象一下把表格的特征列转置过来，然后推进神经网络的左边，由于神经网络中每个神经元的参数 $w$ 和 $b$ 都在被建立时随机赋值了，因此模型可以在最右边输出一个数字，然而这个数字大概毫无意义，它可能是 200，可能是-30，然而真实的是 80，显然，如果我们改变 $w$ 和 $b$ 的取值，就能改变模型最终输出的值，因此我们可以让 $w$ 和 $b$ 的值改变，从而使模型的输出趋近于 80，这个过程就是训练，具体来说是通过梯度下降法来进行训练。从这里可以看出来，机器学习也只能学习到确有关联的数据特征，如果要拟合体重和成绩，结果通常不好并且没有意义。

要注意的是，有时候虽然我们有很多数据，但它们不一定真的存在某种有意义的关系，训练的结果可能很差，甚至有时候神经网络的确得到了一个不错的效果，但是变量间实际上毫无逻辑关系，就像统计学中的伪回归一样。再次强调，一个拥有足够多神经元和足够多层数的神经网络在理论上的确可以拟合所有函数，但它绝不是什么灵丹妙药，因为我们难以解释神经元的行为逻辑，统计学模型可解释性更强。

我们以图 1的网络为例，最左边的输入层是 $x$，由于输入层没有参数，通常也不认为是单独的一层，中间的是一个包含五个神经元的隐藏层，最后是一个神经元构成的输出层，向前传播公式表示为下面的公式组。

这里的 $w,x,b$ 都是以矩阵形式进行运算的，$w_1$ 表示隐藏层权重，$b_1$ 表示隐藏层偏置项，以此类推，$y_{11}$ 表示隐藏层第一次运算结果，$y_{12}$ 表示隐藏层第二次运算结果（激活函数），$y_{21}$ 表示输出层第一次运算结果，没有激活函数。

梯度下降和反向传播

你应该知道正向传播是如何进行的了（吧），在一次正向传播之后会伴随一次反向传播，即通过梯度下降的方法修正，它们一开始是被随机赋值的，我们希望修正它们从而使得模型输出的数字越来越接近已知的真实数据。

我们必须先定义一个损失函数，比如真实值是80，模型预测出为84，那么此时误差不是很大，若模型预测出1000，那么误差就显然很大，但是模型是程序，只认数字，因此我们必须给出一个公式来衡量这种差异。统计学中已经给出了方案，就是方差，如公式 3，也被称为均方差，英文简写 MSE（Mean Square Error），不同的是这里的系数是 $\frac{1}{2}$，其实通常不会一次计算一个样本，而是多个样本同时计算，一起求 MSE，因此严格来说应该是 $\frac{1}{n}$ 或者 $\frac{1}{n-1}$，这样处理是为了方便求导，在求导的时候，平方项和 $\frac{1}{2}$ 会直接抵消，而这个系数只是对损失有缩放，因此没有什么影响。

现在我们有一个衡量损失的函数，如果真实值是 80，预测值是 200，那么 $loss$ 等于 7200，你可以验证一下。我们需要调整 $w,b$ 来使模型的预测靠近真实值，方法就是求导，这一点应该很好理解，我们只需要 $loss$ 对 $w,b$ 求导，就可以知道 $w,b$ 应该如何变化来导致 $loss$ 变小，例如 $\frac{\partial loss(y_{21},y_{true})}{\partial w}=2$，意味着 $w$ 变大一个单位，$loss$ 跟着变大 2 个单位，如果导数值是负的，那就是随着 $w$ 的变大而变小，我们的目的是让它变小，当导数大于 0 的时候，把参数 $w$ 减小一些，反之就增大一些。对 $b$ 也是同样的道理。对于三维或更高维数据来说，求偏导也可以理解为求梯度，由于目的是降低 $loss$ 的值，因此也叫随机梯度下降法，在机器学习模型是一种优化器，英文简称 SGD（Stochastic Gradient Descent），之所以说随机，是因为每次迭代前需要打乱样本，避免参数更新抵消，而优化器比较好理解，调整参数的过程就叫优化，当然也不止于此。

现在看看下面的公式组，这是前面几个公式的集合，我打赌你一定会求这里 $loss$ 的偏导数：

强烈建议你手推一下 $\frac{\partial loss}{\partial w_1}$，然后与下面的结果对比，为了方便一点，$y_{true}$ 写为 $y$，求出来的偏导应该是这样：

公式 5 的所有乘法都是矩阵叉乘，也就是大学线性代数里面那种乘法，求偏导也只是简单的链式求导法则，但是如果你没有接触过矩阵求导，可能会忘记转置：$\frac{\partial Wx}{\partial x}=W^T$。这应该是高等代数的知识，但是你也可以临时学习这个知识点（就像我一样...），我也强烈建议专门抽时间学习高等代数。四个偏导公式里面大部分子式是一样的，比如一式只比二式多了一个 $y_{12}^T$ ，三式只比四式多了一个，利用这个规律可以写自动微分算法，因为算子是可以重复使用的，但这需要很强的算法能力，你也可以写硬代码，比如直接写出手推的公式（但是不同情况就需要改，例如增加层数的情况），会简单一些。

说回正题，$w,b,x$ 都是已知的，直接带入就可以算出偏导的值。在程序中，我们可以用 $w$ 减去 $loss$ 对 $w$ 的偏导值，如果偏导是正的，$w$ 减去一个正数会变小，$loss$ 就会同样的减少，如果偏导是负的，$w$ 减去一个负数，等于 $w$ 变大了，此时 $loss$ 也会减小。求偏导并且修正参数值是从后往前计算的，或者说从右往左，因此也叫反向传播。

一般我们不会直接减去这个偏导值，因为它可能比较大，比如 $w$ 要从 5 修正到 3，然而偏导等于 10，$w$ 减去 10 就被修正到-5，会导致更大的误差并且反复震荡，因此引入一个学习率 $\eta$，比如 0.01，那么 $w=5-10\ast 0.01=4.9$，这提供了一个缓慢修正的过程，不用担心太慢，程序的运行速度是很快的，一旦 $loss$ 变得很小并且不再下降，或者有反向增加的趋势，就应该及时停止程序。

除了梯度下降以外，还有别的衡量方法，只要能够产生相对误差的函数都可以，但是最好选择那些方便求导的误差函数，因为复杂的神经网络需要频繁进行微分计算，消耗大量资源。

实际上，现成的深度学习框架都提供上述所有功能，用户无需自己编写神经网络的各种细节，只需要定义神经网络的深度、每层神经元数量、激活函数类型等，但我仍然鼓励你写出自己的网络。

以上是针对一个简单的只有一个隐藏层的神经网络的计算，更复杂的神经网络也只不过是重复这些过程，但是说实话，我仍然不知道你有没有理解神经网络的运行模式，如果还不太懂，可以搜索一些可视化神经网络机制的视频，我相信有很多。

梯度爆炸和梯度消失现象

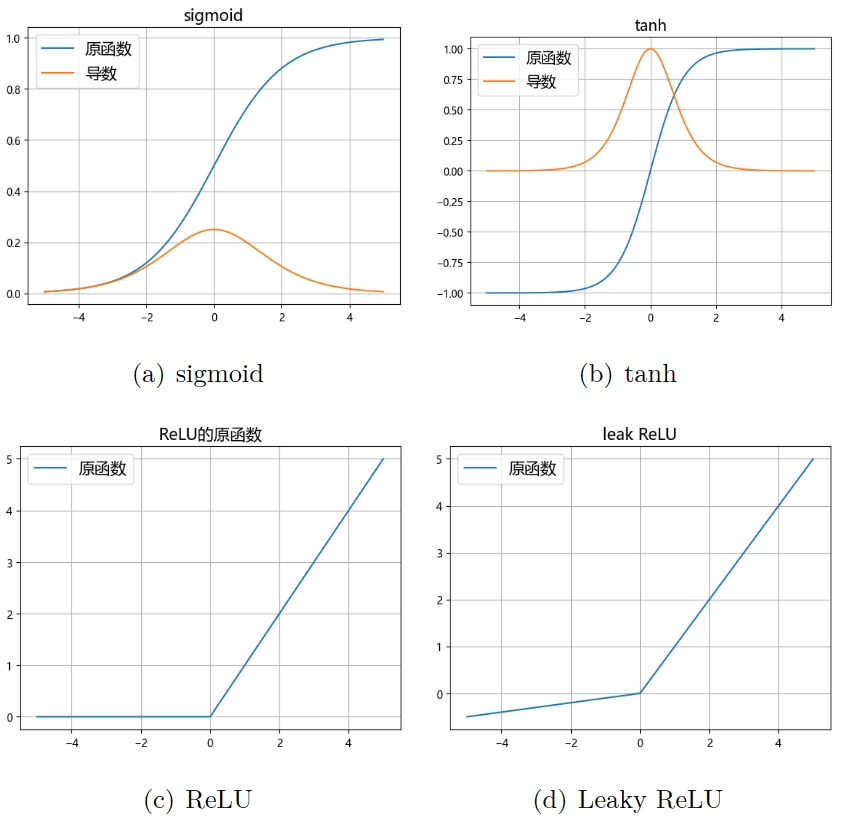
由于每个神经元是由一个简单的线性方程和一个激活函数组成的，而线性方程的求导极为简单，x 的导数就等于它的系数，比较麻烦的是激活函数，由于求导是链式的，如果有多层网络，就会把多次求导的结果累乘起来，复杂的网络可能要累乘几十次甚至几百次，这会导致一些问题，比如函数的导数的取值范围是(0, 0.25]，当 x 很大或者很小时，梯度就接近于0，再乘以学习率，那么梯度就非常小，导致学习效率很低，的导数取值范围是(0, 1]，同样面临梯度消失的问题。在 x＞0时，梯度等于1，无论乘多少次都是1，当然 x<0时，梯度消失，因此后人也有改进为函数 Leaky relu，在 x<0时给一个很小的梯度，不至于消失，但是至今仍然是最常用的激活函数之一，在卷积神经网络中，最常用的是。梯度爆炸就是梯度大于1的情况，经过累乘会导致梯度极大，这都与激活函数的选择有关。

神经网络代码实现

现在神经网络框架的集成程度已经相当高，只需要简单几行代码就可以建立一个简单的神经网络。常用的框架有 Pytorch，Tensorflow 和 Keras 等，其中 Keras 已经被集成到 Tensorflow。读者只需要选一个框架学习即可，这里推荐 Pytorch，因为其社区支持很好，学术界也普遍采用该框架，但笔者目前主要使用 Tensorflow。注意，学习本节需要读者对 python 编程有一定的掌握，并且要熟悉 numpy，matplotlib 等重要包的使用。

现有框架实现神经网络

每个框架都有多种写法，这里仅展示比较简单，便于理解的进行展示，你需要综合你前面全部所学去理解这些代码，因此有一定难度，但仍然推荐看看如何用现成框架实现，尽管不推荐重复造轮子，但最好知道轮子的原理。

回归/拟合任务

一般的回归任务，例如对上表来说，需要拟合期末考试分数，输入的是前两次模拟考试的分数，大小为 2，那么应该提前准备好 x_train，它包含前面两个字段（对于任何即将倒入神经网络的数据来说，都不要专门包含一个 index 字段，这里只是模仿 excel 软件中的显示方便阅读），同时，y_train 就包含最后一个字段"期末考试"。我还单独准备了验证集数据 x_valid, y_valid，也可以不手动准备，参考下一节分类任务代码。验证集的作用是方便调整模型，例如神经元层数或者个数，因为我们用训练集进行训练，要验证它的效果，就需要在一个同分布的陌生的数据中去测试，验证集和测试集来源于同一个数据，因此它们的分布是一样的，此外还有测试集，有时候可以不用准备，因为测试集相当于在实际问题中应用模型，有时候我们只需要评估效果，用验证集就够了。关于如何整理表格并且分字段赋值到另一个变量中，请参考 pandas 包的文档。

# 基于tensorflow实现
import tensorflow as tf
from tensorflow import keras
model = keras.models.Sequential([
  keras.layers.Dense(30, activation="relu", input_shape=[2]),
  # 第一层30个神经元，激活函数ReLU，8个神经元，输入大小2
  keras.layers.Dense(20, activation="sigmoid"),
  keras.layers.Dense(1)
  # 最后一层输出层，1个神经元，没有激活函数
 ])
model.compile(loss="mse", optimizer=keras.optimizers.SGD(learning_rate=1e-3))
# 编译模型，损失函数为mse，优化器为SGD，其中学习率0.001
history = model.fit(x_train, y_train, epochs=10,
validation_data=(x_valid, y_valid))
# 训练模型，输入x_train y_train，训练10个迭代，验证数据集为x_valid, y_valid

在 model 的最后一层有一个神经元，没有激活函数，因为在回归或者拟合任务中，输出就是一个值，需要拟合的是期末考试成绩，只是一个值，如果在最后一层采用 sigmoid 激活函数，那么输出就在 0 到 1 之间，这不符合现实，或者加一个 ReLU，小于 0 的输出将直接变成 0，在本例中成绩分数一定大于等于 0，但是在其他任务中则完全有可能小于 0，不必多此一举。

训练模型的命令是 model.Fit()，输入 x 和 y，模型会自动依据这两个数据进行优化，比如梯度下降，这里还有其他参数，可以参考相关文档。

分类任务

我们虚构一个分类任务，如下表，现在有三个特征和一个标签，"花的种类"有四种，用 1，2，3，4 来表示，那么同样的 x 应该是包含前三个字段的表格 y 包含"花的种类"，这里没有单独划分验证集，而是在函数 fit() 中指定 validation_split=0.3，表示输入的数据中有 30% 用于验证。

# 基于tensorflow实现
import tensorflow as tf
from tensorflow import keras
model = keras.models.Sequential([
  keras.layers.Dense(30, activation="relu", input_shape=[3]),
  # 输入的大小是3，对应三个特征
  keras.layers.Dense(20, activation="sigmoid"),
  keras.layers.Dense(4, activation="softmax")
 ])
model.compile(loss="sparse_categorical_crossentropy", optimizer='nadam', metrics=["accuracy"])
# 编译模型，损失函数为二元交叉熵，优化器为nadam
history = model.fit(x, y, epochs=10,
validation_split=0.3)

最后有 4 个神经元输出，激活函数用 softmax，如公式 6，这是 sigmoid 的多分类改进，它们的输出区间是一样的，都是 (0,1)，分子是全部分母中的一个，这里有四个分类，因此 $n=4$，一共有四个分母。模型输出的是 4 个在 (0,1)区间的概率值组成的数组，分别代表样本属于四个类别的概率。此外损失函数也变成了二元交叉熵而非 MSE，这是分类任务的损失度量方法，优化器变成 nadam，这是现在最先进的梯度下降方法之一，我们还加了个衡量标准 accuracy，你暂时不需要了解太多这些新知识，先学会使用和观察效果即可。

从零开始手写神经网络

我们需要引用下面的包，如果你没有这些包，则需要在终端中键入命令 pip Install numpy，若缺少其他包，也要用类似方法安装。

import numpy as np 
import pandas as pd 
import matplotlib.pyplot as plt

先准备数据，在-2 到 2 之间等距取 1000 个 x 点，y=2 sinx，并且在 y 上加一些噪声，同时还要给 x 和 y 加一个维度。

x0 = np.linspace(-2, 2, 1000)
y0 = 2 * np.sin(x0)
y0 += 0.32 * np.random.randn(y0.shape[0]) # 加噪声

x = x0[:, np.newaxis]
y = y0[:, np.newaxis]

写一个 loss 函数度量损失，只要输入一个或一组预测 y 值，再输入一个或一组真实 y 值，此函数返回 $mse$ 值。

def mse(yl, y0):
 return ((yl - y0)**2).sum()/yl.shape[0]

我们用统计学的最小二乘法，也就是公式法，求出线性回归的函数，以此作为基准，在机器学习领域经常需要建立一个基准，以验证模型是否存在改进。

b2 = float((len(y0)*(x0*y0).sum(0) - y.sum(0)*x0.sum(0)) /
(len(x0)*(x0**2).sum(0) - (x.sum(0)**2)))

b1 = float(y0.mean() - b2 * x0.mean())
print('回归方程为: y = {:.2f} + {:.2f} * x'.format(b1, b2))
# 数据是标准化的，因此截距项为0

回归方程为: y = 0.01 + 1.31 * x

画出最小二乘法给出的函数图像

yl = []
for i in x0:
yl.append(b1 + b2 * i)
yl = np.array(yl)
plt.scatter(x0, y0, label='原始点')
plt.plot(x, yl, 'r', label='最小二乘法回归线, 损失{:.3f}'.format(baseline))
plt.legend(fontsize='13')

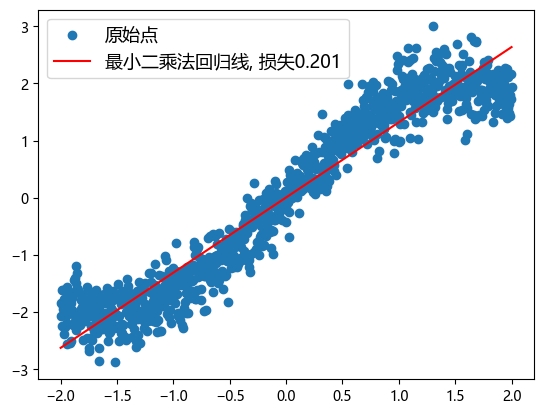
我们再用 Keras 来训练一下，作为基准，也就是对比，其结构与我后面手搓的神经网络一致，即一个隐藏层，包括 5 个神经元，输出层有 1 个神经元。

from tensorflow import keras
model_tf = keras.models.Sequential([
        keras.layers.Dense(5, input_shape=[1,], activation='sigmoid'),
        keras.layers.Dense(1),
    ])
model_tf.compile(loss='mse', optimizer=keras.optimizers.SGD(0.01))
history = model_tf.fit(x, y, epochs=50, validation_split=0.3)
# 用百分之三十的数据作为验证集，每次迭代会被自动打散并且分割数据

pd.DataFrame(history.history).plot(figsize=(8, 5)) # 画出损失图像
# 画出对比图象
plt.scatter(x0, y0, c='gray', label='原始点')
plt.plot(x0, yl, 'r', label='最小二乘法回归线, MSE为 {:.3f}'.format(baseline))
plt.plot(x0, y_tf, 'green', label='keras神经网络, MSE为 {:.3f}'.format(keras_mse))
plt.legend(fontsize='10')

得到下面两张图，左边是损失情况，其中橙色的线是验证损失，蓝色的是训练损失，具体含义在 03_机器学习效果评估 详细解释，右边可以看到黄色线是 Keras 的训练结果。

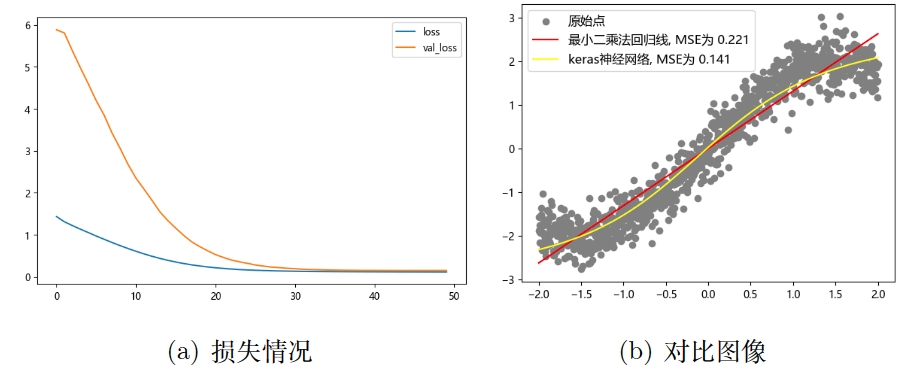
下面是手搓神经网络的完整代码，如果还没有学类封装编程，可以先跳过。原代码可以通过 手搓BP神经网络 在线浏览。

class BP():
    def __init__(self) -> None:
        pass

    def activate(self, t):
        '''
        激活函数， sigmoid 或 relu
        '''
        if self.activator == 'sigmoid':
            return 1/(1+np.e**(-t))
        if self.activator == 'relu':
            return np.maximum(t, 0)

    def input_forward_hidden(self, x):
        ''' 
        输入层到隐藏层
        y11 = w1x1 + b1 \\
        输出 y12, 大小 (5, 1) -> (神经元数量, x数量) (y11在反向传播用不到)
        '''
        x = x[:, np.newaxis]
        y11 = self.w1 @ x + self.b1 # 叉乘**
        y12 = self.activate(y11)
        return y12

    def hidden_forward_output(self, y12):
        ''' 
        隐藏层到输出层, 这里无需激活函数
        y21 = y12 * w2 + b2 \\
        网络最终输出 y21, 大小 (1, 1) -> (神经元数量, y数量)
        '''
        y21 = self.w2 @ y12 + self.b2 # 叉乘**
        return y21

    def metrics(self, y_p, y_t, loss='mse') -> float: # type: ignore
        '''
        计算误差
        '''
        if loss == 'mse':  # 均方差
            return (((y_p - y_t)**2).sum()/2)

    # 下面是四个参数的反向传播更新，公式是手推链式求导直接写的**
    def update_w2(self, yt, y21, y12, lr=0.02):
        '''
        更新输出层权重,先是输出层w2
        '''
        delta_w2 = (y21 - yt).sum() * y12.T
        return self.w2 - lr * delta_w2

    def update_b2(self, yt, y21, lr=0.02):
        delta_b2 = (y21 - yt).sum()
        return self.b2 - lr * delta_b2
  
    def update_w1(self, yt, y21, y12, x, lr=0.02):
        delta_w1 = (y21 - yt).sum() * self.w2.T * y12 * (1 - y12) * x.T
        return self.w1 - lr * delta_w1
  
    def update_b1(self, yt, y21, y12, lr=0.02):
        delta_b1 = (y21 - yt).sum() * self.w2.T * y12 * (1 - y12)
        return self.b1 - lr * delta_b1
  
    def fit(self, x, y, activator):
        self.w1 = np.random.randn(20, 1) 
        # 👆大小规则：本层神经元数量, 一次输入一个，可以用batch一次多个**
        self.b1 = np.random.randn(5, 1) 
        # 👆大小规则：本层神经元数量, 一维神经网络就一层**
        self.w2 = np.random.randn(1, self.w1.shape[0]) 
        # 👆大小规则：本层神经元数量，上一层神经元数量**
        self.b2 = np.random.randn(1, 1) 
        # 👆大小规则：本层神经元数量, 一维神经网络就一层**
        self.y = y
        self.x = x
        self.mse = 0
        self.activator = activator
    
        # 统计损失
        self.list_mse = []
    
    def train(self, epochs:int, lr=0.02, loss_type='mse', target_error=0.0001):
        for _ in range(epochs): 
            for xs, yt in zip(self.x, self.y): # x_sample, y_true(label)
                y12 = self.input_forward_hidden(xs)
                y21 = self.hidden_forward_output(y12)
                self.w2 = self.update_w2(yt, y21, y12, lr)
                self.b2 = self.update_b2(yt, y21, lr)
                self.w1 = self.update_w1(yt, y21, y12, xs, lr)
                self.b1 = self.update_b1(yt, y21, y12, lr)
                self.mse = self.metrics(y21, yt, loss_type) # type: ignore
            self.list_mse.append(self.mse)
            
            if self.mse <= target_error:
                print('✅ 共{:d}轮, 达到目标损失, \
                    最终损失E={:.5f}'.format(_+1, self.mse))
                break
        
            if _ > 15 and np.mean(self.list_mse[-20: -1]) < self.list_mse[-1]:
                print('✅ 共{:d}轮, 损失反向增大，自动停止, \
                      最终损失E={:.5f}'.format(_+1, self.mse))
                break
        
            elif _ == epochs - 1 and self.mse > target_error:
                print('❌ 共{:d}轮, 最终损失E={:.5f}, \
                    未达到目标损失 {:.5f}'.format(_+1,self.mse, target_error))
                break
        
    def fit_transform(self, x, y, epochs:int, lr=0.01, activator='sigmoid', 
                      loss_type='mse', target_error=0.00):
        '''
        epochs: 最大轮次, 每一轮次过一次全部数据 \\
        lr: 学习率, 默认0.01 \\
        activator: 'sigmoid' 或 'relu'(尚未配适反向传播, 勿用) \\
        loss_type: 损失类型, 目前仅有 "mse"
        '''
        self.activator = activator
        self.fit(x, y, self.activator)
        self.train(epochs, lr, loss_type, target_error)
    
    def predict(self, new_x):
        y_lst = []
        for i in new_x:
            y0 = self.input_forward_hidden(i)
            y1 = self.hidden_forward_output(y0)
            y_lst.append(y1)
        y_lst = np.array(y_lst)
        y_lst = y_lst.reshape(y_lst.shape[0])
        return y_lst

调用并且训练此类：

model = BP() model.fit_transform(x, y, 100, lr=0.0005,
activator='sigmoid')

√ 共28轮, 损失反向增大，自动停止, 最终损失E=0.00238

查看损失情况和对比图：

plt.title('损失情况', fontsize=15)
plt.ylabel('损失', fontsize=15)
plt.xlabel('训练回合', fontsize=15)
plt.grid()
plt.plot(model.list_mse, label='神经网络')
yp = model.predict(x)
plt.text(0, -2.5, 'y=2sinx', fontsize=15)
plt.scatter(x, y, s=3, c='gray', label='原散点')
plt.plot(x0, yl, 'r', label='最小二乘法回归线, mse = {:.3f}'.format(baseline))
plt.plot(x0, y_tf, 'green', label='keras神经网络, mse = {:.3f}'.format(keras_mse))
plt.plot(x, yp, c='b', label='手搓神经网络, mse = {:.3f}'.format(bp_mse))
plt.legend(fontsize=10)

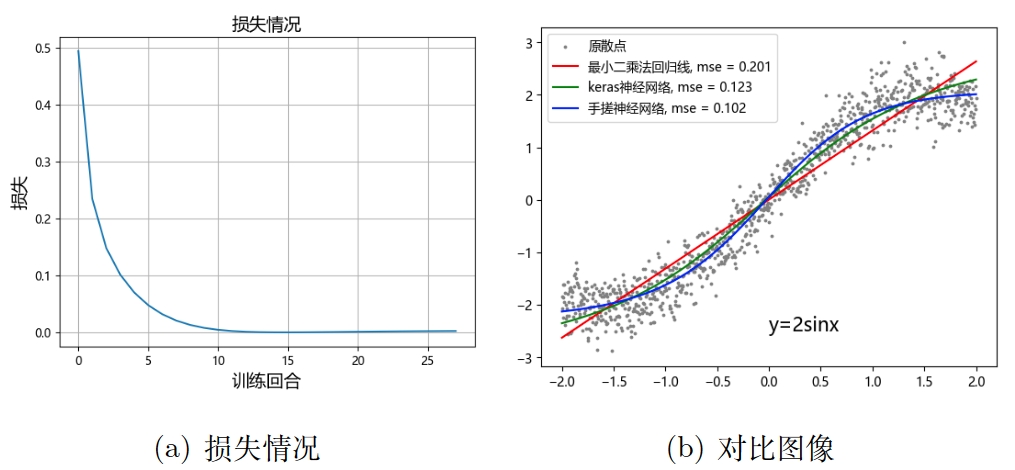
与图6类似，图7左边表示损失变化的情况，但我没有实现展示验证集损失的效果，右边是三种方法的拟合对比图，可以看到蓝色线条表示的手搓神经网络的拟合效果是不错的。你还可以检查一下我的 update_w1() 等其他函数是否与前面的偏导公式一致。

我没有对整个手搓代码进行详细的分段解释，这里仅作一些提示，比如激活函数是需要定义好的，误差函数也可以方便地引用，有点类似于搭积木，如果你很熟悉神经网络所需的各个部件，那么你就自然而然地想写出每一个部件的函数，这个思路是没错的，但是如果仔细看我网络的实现方法，例如 input_forward_hidden()，会发现我只是在里面进行张量计算，而不是"定义 5 个实际的神经元函数"，也许这也行得通，但我没有尝试过，我也并不是算法天才😨。在我的框架中，要改变神经元数量需要在 fit() 方法中进行修改，而且不方便修改层数，反向传播写的是硬代码而非自动微分技术。

自己写神经网络是需要花不少功夫的，很多人在短时间内就可以理解神经网络的原理，但是真的动手时会发现很多问题，代码会出现很多 bug，都需要自己一遍又一遍调试，我直到基本学完深度学习基础之后才回过头来尝试手写神经网络代码，本以为应该是得心应手，毕竟调包的时候手到擒来，但实际上困难重重，你需要对每一个细节进行把关，任何一个理解错误都可能导致整个模型功亏一篑，同时，这也是对你编程能力的重要挑战。